Fonksiyonel Programlama I - Lambda Kalkülüs I

Structure and Interpretation of Computer Programs kitabının kapağından.

Fonksiyonel programlama Lambda Kalkülüs temelleri üzerine inşa edilmiş bir yaklaşımdır. Dolayısıyla fonksiyonel programlamayı kullanmaya başlamadan önce bu temeli atmak yapımızın sağlamlığı ile doğrudan ilişkili olacaktır.

Kalkülüs

Latincede hesap tutmak için kullanılan çakıl taşlarına calculus denirmiş. Bugün ise bilimsel bir kavram olarak Kalkülüs (hesap, işlence), bir hesaplama veyahut muhakeme yöntemini ifade eder. Kalkülüs sembollerin işlenmesi ve manipüle edilmesiyle ilgilidir. Ancak sembollere ilişkin değildir; yani sembollere istediğimiz anlamı verebilir, istediğimiz anlam kümesini bir sembolle ifade edebiliriz.

Lambda Kalkülüs

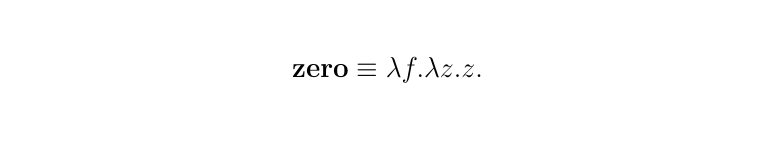sıfırın lambda calculus ile gösterimi. (bkz: church encoding)

Lambda kalkülüs (λ-Kalkülüs, Lambda Calculus) fonksiyonları soyutlama (abstraction), bağlama (binding), uygulama (application) ve ikame etme (substitution) kavramları üzerine kurulu bir hesaplama modelidir. Turing makineleri’nin de yaptığı gibi lambda kalkülüs; hangi problem veya problem kümelerinin çözülebilir olduğunu belirlemeye çalışan etkili hesaplanabilirlik (effective computability) kavramını formalize eden bir nosyondur. Ancak şunu eklemekte fayda var; lambda kalkülüs turing makinesinin aksine, fiziksel bir makine fikri değil, daha soyut bir tasarımın ürünüdür.

Lambda kalkülüs herhangi bir tek şeritli turing makinesini taklid edebildiği için; turing complete, yani hesaplama açısından evrenseldir (universal computability). Ayrıca daha sonraları, turing makinesi ve lambda kalkülüsün birbirine denk kuramlar olduğu da farkedilmiştir. (bkz: Turing Equivalence, Church-Turing Thesis)

Lambda kalkülüs’ün ilham aldığı Gödel’in özyineli fonksiyonları (recursive functions) bir başka turing complete hesaplama modelidir.

Lambda Kalkülüs, bugün kendisinden çok daha popüler Alan Turing’in hocası, ABD’li matematikçi Alonzo Church tarafından 1930’lu yıllarda geliştirilmiştir. (bkz: Lambda Calculus, Computability, Turing Completeness, Turing Machine, Church-Turing Thesis, Alonzo Church, Alan Turing)

Lambda kalkülüsün kullanımına geçmeden önce, kullandığımız kavramların mefhumunun zihinlerimizde aynı şeye tekabül ettiğini doğrulamak üzere bazı temel kavramlara gözden geçirelim

Fonksiyon Nedir?

Genel tanımıyla fonksiyon, tanım kümesindeki bir elemanın değer kümesindeki yalnızca tek bir elemanla arasındaki bağıntıdır. Daha somut bir anlatım ile ise: sahip olduğumuz bir bilgiden (girdi, input, tanım kümesi, domain) bizi bir başka bilgiye (çıktı, output, değer kümesi, range) ulaştıran sürece fonksiyon denir.

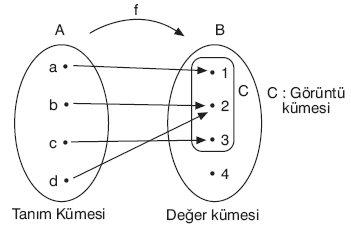
Örnek olarak bir f fonksiyonu farz edelim. Parantez içindeki değer girdi, Sağdaki değer ise çıktı olacak şekilde:

f(1) = A
f(2) = B
f(3) = C

Buradaki can alıcı husus, f foksiyonu girdi olarak aldığı her 1 değeri için her zaman istisnasız bir şekilde çıktı olarak A değeri verecektir. Yani fonksiyona verilen bir girdi bize her zaman aynı değer olarak geri verilecektir (bkz: referential transparency).

Yani g,

g(1) = A
g(1) = B
g(2) = C

geçerli bir fonksiyon değildir. Ancak bunun yanı sıra h,

h(1) = T
h(2) = T
h(3) = T

geçerli bir fonksiyondur. Örnek olarak bir kare fonksiyonu negatif ve pozitif değerler için aynı değeri döndürebilir. Veyahut 100’den küçük sayıları belirleyen bir fonksiyon.

Yine bir f fonksiyonu farz edelim

f(x) = x + 1

Fonksiyon, değeri ne olursa olsun x değerine 1 ekleyecektir. Bu fonksiyonu bir değere uygularsak, değer x’in yerine geçecektir (substitution):

f(6) = 6+ 1

Fonksiyon girdisinin çıktıya nasıl eşlendiğini (mapping) f’e 6 değerini uygulayarak, 6+1=7 olarak anlıyoruz

f(6) = 7

Lambda Kalkülüsün Yapısı

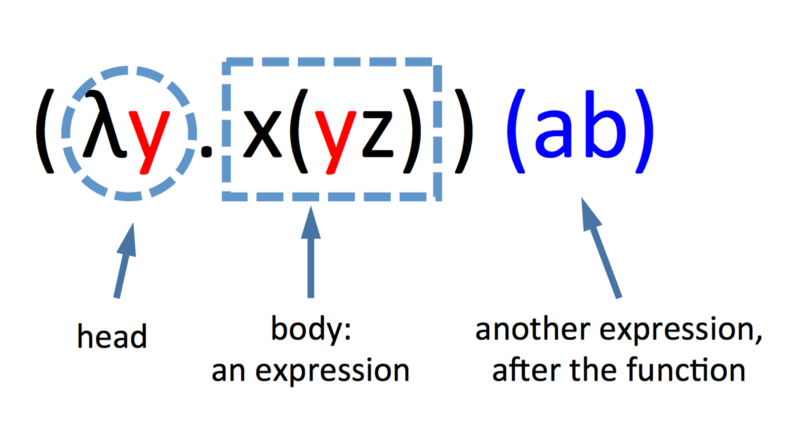Lambda kalkülüs, temel olarak üç bileşenden oluşur; ifadeler (expression), değişkenler (variable) ve soyutlama (abstraction). İfadeler, tüm bunları kapsayıcı büyük kümedir. İfadeler; değişkenler, soyutlama ve bunların kombinasyonlarından oluşabilir. Soyutlama ise fonksiyonlardır. Fonksiyonlar baş (head, lambda) ve gövdeden (body) oluşur. Girdi argümanları bu gövde üzerine uygulanır. En basit formuyla bir fonksiyon:

λx.x

Lambda ifadesinden sonraki x değişkeni parametredir ve gövdedeki aynı değişkenin diğer tüm örnekleriyle ilişkilendirilir. Nokta (.) baş ve gövdeyi birbirinden ayırır.

Fonksiyonlardan bahsederken fonskiyonlarımıza f, g gibi isimler verdik. Fakat lambda fonksiyonları isimsiz fonksiyonlardır (anonymous function). İsimsiz fonksiyonlar, isimli fonksiyonlar gibi başka fonksiyonlar tarafından çağırılamaz.

Alfa Eşitliği

h(1) = T
h(2) = T
h(3) = T

λx.x
λa.a
λt.t

Alfa eşitliği (Alpha Equivalence), değişkenlerin (yukarıda x, a ve t) anlamsal olarak hiçbir şey ifade etmediğiyle ilgilidir. Bu üç ifade de aynı fonksiyonu işaret eder.

Beta İndirgemesi

Bir argümanın fonksiyona uygulanması ve gövde üzerindeki bağıl değişkenlerin (bound variable) yerine geçmesi sürecine (substitution) beta indirgemesi (β-Reduction) diyoruz. Bu süreçte zaten tek işi değişkenleri gövdeye bağlamak olan baş kısmından da kurtulmuş oluyoruz. Yine aynı fonksiyonu alalım:

λx.x

Şimdi bu fonksiyonumuza bir beta indirgemesi uygulayalım. Fonksiyona argüman olarak bir sayı verelim ve indirgeyelim:

(λx.x) 5
5

Parantezin sağ tarafına yazdığımız değeri argüman olarak x’in yerine koyuyoruz. Ve baş kısmından kurtulduğumuzda 5 sonucuna ulaşıyoruz.

Aslında burda yaptığımızı isimli bir fonksiyonla gösterecek olursak:

f(x) = x
f(5) = 5
5

şeklinde basit bir şekilde ifade edebiliriz. Bu bildiğimiz birim fonksiyona (identity function) bir örnekti. Peki bir birim fonksiyonu argüman olarak başka bir birim fonksiyona versek?

(λx.x)(λy.y)

Burda yeni bir sentaks kullanacağız. Tüm x’lerin yerine z koyulacağını belirtmek için [x := z] şeklinde bir gösterim kullanacağız. Beta indirgemesi ise şöyle olacak:

(λx.x)(λy.y)
[x ∶= (λy.y)]
λy.y

Uygulayacak argümanımız kalmadığı için indirgemenin en son hali bize argüman olarak verdiğimiz birim fonksiyon olarak dönüyor. Peki o zaman bir argüman daha verip ve beta indirgemesini uygulayalım:

(λx.x)(λy.y)z
[x := (λy.y)]
(λy.y)z
[ y := z]
z

Yine fonksiyona uygalayacak argüman kalmadığı için indirgemeyi sonlandırdık. Özetle; beta indirgemesi, fonksiyona geçirebileceğimiz argüman kalmadığı veyahut değerlendirilecek baş (λ) kalmayıncaya kadar sol içten dışarı doğru uygulanır.

Birden Çok Argüman (Currying)

Şu ana kadar farkettiğiniz üzere bir lambdaya sadece bir değişken bağlayabiliyoruz. Çoklu argüman kullanmak istediğimizde ise yapmamız gereken iç içe geçmiş lambda ifadeleri kullanmak. Currying ismi Haskell Curry’e ithafen koyulmuş bir isim de olsa bu tekniği ilk ortaya koyan kişi olan Moses Schönfinkel’e ithafen “Schönfinkelisation” olarak da geçer. Currying çok daha iyi bir isim tercihi sanırım :)

Bir örnek ile gösterecek olursak:

λxy.xy

iç içe iki değişkenli bir lambda ifadesinin kısa biçimde yazılmasıdır:

λx.(λy.xy)

Fonksiyona argüman vererek bir örnekle somutlaştıralım neden bahsettiğimizi:

(λxy.xy) 5 10
(λx.λy.xy) 5 10
[x := 5]
(λy.5y) 10
[y := 10]
5 10

Bağlı ve Bağımsız Değişkenler

Gövdedeki değişkenler baş kısmına bağlanıyorsa, yani baş kısmında da varsa bunlara bağlı değişkenler (bound variable), eğer sadece gövdede yer alıyorsa bunları bağımsız değişkenleri (free variable)olarak adlandıyoruz.

λx.xy

Bu fonksiyona beta indirgemesi uygulayarsak bakalım ne oluyor, z değerini argüman olarak verelim:

(λx.xy) z
[x := z]
zy

z ve y değerleri hakkında daha fazla birşey yapamadığımız için bu aşamada beta indirgemesini sonlandırıyoruz.

Burda alfa eşitliğine bir gönderme yapmakta fayda var;

λx.xz
λx.xy

ifadeleri z ve y’nin farklı değerler olabileceğinden dolayı birbirine eşit değilken,

λxy.yx
λab.ba

ifadeleri birbirine eşittir.

Normal Form

Eğer bir ifadeye daha fazla beta indirgemesi uygulayamıyorsak ifademiz normal formda (beta normal form) demektir. Yani bir nevi programın çalıştırılmış halidir diyebiliriz. Örneğin daha somut bir örnekle gösterecek olursak 2 değeri 4/2 ifadesinin normal formudur. Normal form, eksiltilecek (indirgenecek) birşey kalmaması demektir. Örneğin ((5 * 3) + 19) + 1 ifadesinin normal formu 35’tir; çünkü daha yalın bir hali yoktur.

Iraksaklık

Tüm ifadeler beta normal forma indirgenebilir mi? Beta indirgenmesi tamamen uygulanmış da olsa bazı ifadeler normal forma indirgenemez. Bu ifadeleri ıraksak (divergent) olarak nitelendiriyoruz. Örneğin şöyle bir ifadeyi indirgemeye çalışalım:

(λx.xx)(λx.xx)
[x := (λx.xx)]
(λx.xx)(λx.xx)
[x := (λx.xx)]
(λx.xx)(λx.xx)
...
...
...

Yerine koymayı uygulayarak x’in yerine (λx.xx) koydukça ilk başladığımız yere geri dönüyoruz. Yani yakınsamıyoruz, ıraksıyoruz.